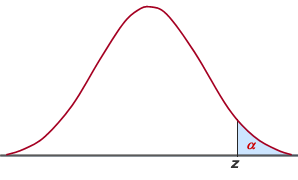
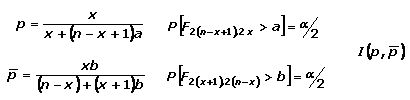 Tabla para determinar los valores característicos de una
distribución normal: z y |
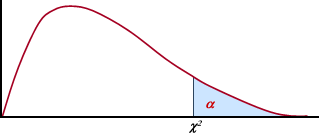
Tabla para determinar los valores característicos de una
distribución ji-cuadrado: |
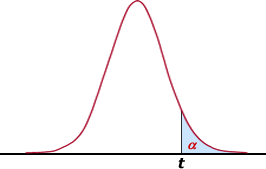
Tabla para determinar los valores característicos de una
distribución t de Student: t
y |
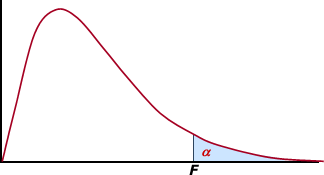
Tabla para determinar los valores característicos de una
distribución F de Fisher-Snedecor: Fy
|
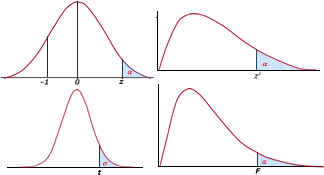
Hoja de cálculo para determinar los parámetros característicos de diferentes distribuciones: normal, normal estandarizada, ji-cuadrado, t de Student y F de Fisher y Snedecor. |
MATERIALES DE ESTADÍSTICA APLICADA A LA BIOINFORMÁTICA
Tablas de distribuciones de probabilidad (requiere Adobe Acrobat Reader)
Distribución acumulada de la distribución normal estándar N(0,1)
Distribución acumulada de la distribución de la ji-cuadrado
Distribución acumulada de la distribución t de Student
Distribución acumulada de la distribución F de Fischer-Snedecor
Hoja de cálculo MS-Excel distribuciones: normal, ji-cuadrado, t y F
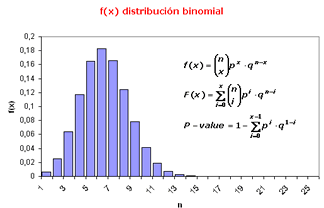
Se realizan n procesos o experimentos
de Bernoulli de manera que la probabilidad de éxito sea
la misma en cada prueba, es decir, consideremos n
variables aleatorias independientes de Bernoulli X1,
X2,...,Xn con probabilidad de éxito p1=p2=...pn. |
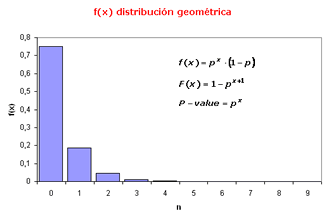
Si X es una variable aleatoria binomial de probabilidad p, las probabilidades de que al realizar un ensayo se presente el suceso x es p y la de que no se presente es (1-p); la probabilidad de que el suceso x se presente en los n-1 primeros ensayos y que no se presente en el enésimo sigue una distribución geométrica. |

Un experimento en el la probabilidad de éxito es p y de fracaso (1-p). Se repite el experimento de forma independiente hasta que observamos m fallos. La variable aleatoria X que mide el número de éxitos hasta obtener el emésimo fracaso se dice que sigue una distribución binomial negativa. |
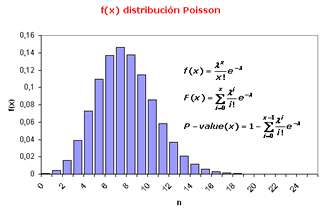
Una distribución binomial cuando n
es grande y p pequeño podemos
aproximarla por la distribución de Poisson con parámetro
|
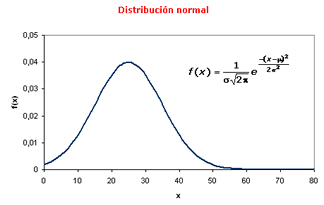
Distribución normal com media |
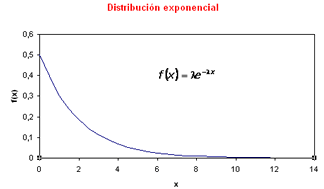
Distribución exponencial de parámetro 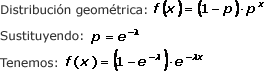
|
Estudio gráfico de las funciones de distribución (Hojas de cáculo MS-Excel)
Distribución binomial
Distribución geométrica
Distribución binomial negativa
Aproximación de Poisson
Distribución normal
Distribución exponencial
Hojas de cálculo de MS-Excel para la realización de pruebas de conformidad
Conformidad de la media (normal) con 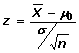 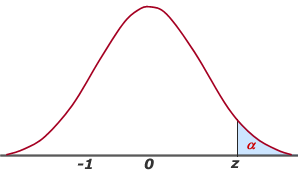
Conformidad de la media (normal) con 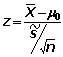

Conformidad de la media (normal) con 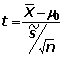  |
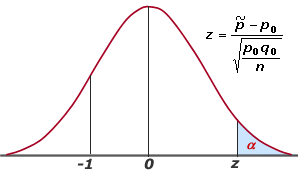
Conformidad de la proporción de una muestra con la proporción de la población. |
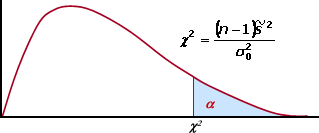
Conformidad de la varianza de una muestra con la varianza de la población. |
Pruebas de conformidad de la media
Pruebas de conformidad de proporciones
Pruebas de conformidad de la varianza
Hojas de cálculo de MS-Excel para el cálculo de intervalos de confianza
Intervalo de confianza de la media (normal) con 
Intervalo de confianza de la media (normal) con 
Intervalo de confianza de la media (normal) con  |
Intervalo de confianza de proporciones.
|
Intervalo de confianza de una varianza. 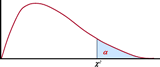
Intervalo de confianza del cociente de varianzas. 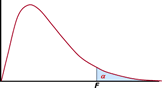 |
Intervalos de confianza de medias
Intervalo de confianza de proporciones
Intervalos de confianza de varianzas
Hojas de cálculo de MS-Excel para la realización de pruebas de contraste de hipótesis
Contraste de dos medias distribución normal y 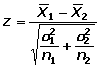

Contraste de dos medias con distribución normal y
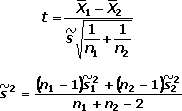  Contraste de dos medias con distribución normal y
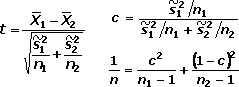 
|
Contraste de medias muestras dependientes con distribución
normal y 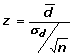

Contraste de medias muestras dependientes con distribución
normal y 
 Contraste de medias muestras dependientes con distribución
normal, 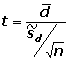  |
Contraste de proporciones con p1 y p2 conocidas. 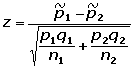

Contraste de proporciones con p1 y p2 desconocidas. 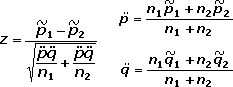 
|
Comparación de varianzas.
 |
Contraste de dos medias con observaciones independientes
Contraste de dos medias con observaciones dependientes
Constraste de proporciones
Contraste de dos varianzas
Hojas de cálculo de MS-Excel para la realización de pruebas estadísticas en Bioinformática
Prueba binomial global: podemos
asumir la similitud entre dos secuencias utilizando una prueba
global, que consiste en contar el número de emparejamientos
correctos que se dan entre las dos secuencias. 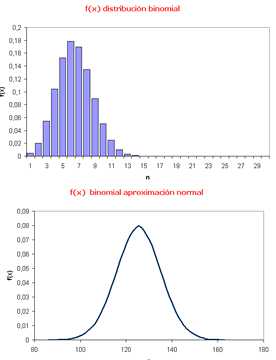 |
| Razón de probabilidad o relación de probabilidades:
en muchos casos pueden realizarse comparaciones entre la hipótesis
nula y la alternativa utilizando como prueba el logaritmo de
la relación de probabilidades (probabilidad de la hipótesis
alternativa y la probabilidad de la hipótesis nula).  |
Prueba para comprobar los éxitos locales (A local sucess
runs test): se aplica a la comparación de secuencias
se fundamenta en la longitud de los éxitos locales. Este
estadístico se define como el máximo de la longitud
de bases emparejadas seguidas. Es un estadístico local
que sigue una distribución del máximo de n distribuciones
geométricas: 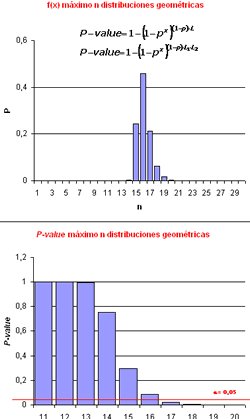 |

Conformidad de la varianza de una muestra con la varianza de la población. |
BLAST Basic Local Alignment Search Tool desarrollada por Altschul, S.F., Gish W., Miller W., Myers E.W., and Lipman D.J. (J. Mol. Biol. 1990: 215:403-10) es un programa que se utiliza para realizar estudios de emparejamiento de ácidos nucleicos y mira la longitud del segmento máximo de emparejamiento correcto. 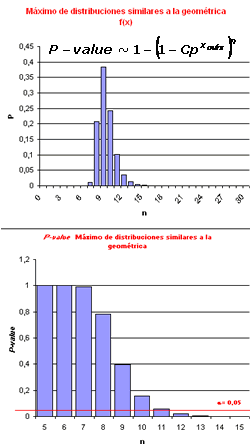 |
BLAST Basic Local Alignment Search Tool desarrollada por Altschul, S.F., Gish W., Miller W., Myers E.W., and Lipman D.J. (J. Mol. Biol. 1990: 215:403-10) es un programa que se utiliza para realizar estudios de emparejamiento de proteínas y mira la longitud del segmento máximo de emparejamiento correcto. 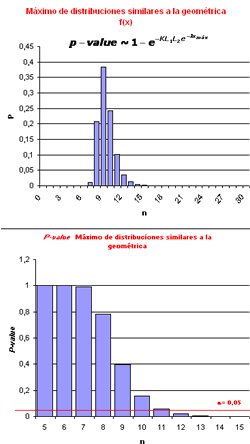 |
Prueba binomial global y su aproximación por una normal
Relación de probabilidad - distribución binomial y su aproximación por una normal
Prueba de éxitos locales con la misma longitud y con diferente longitud
Alineamiento de fragmentos de ADN por BLAST con la misma longitud y con diferente longitud
Alineamiento de fragmentos de proteínas por BLAST
 [English
version] [English
version] |

 (en la práctica la aproximación
se puede realizar cuando n>50 y
p<0,1).
(en la práctica la aproximación
se puede realizar cuando n>50 y
p<0,1).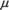 y desviación estándar s.
y desviación estándar s.